CLASS 9 ICSE/CBSE BOARDS CIRCLE FULL CHAPTER

Circle Exercise Ex. 17(A)

Solution 1

Let AB be the chord and O be the centre of the circle.

Let OC be the perpendicular drawn from O to AB.

We know, that the perpendicular to a chord, from the centre of a circle, bisects the chord.

AC = CB = 3 cm

Solution 2

Let AB be the chord and O be the centre of the circle.

Let OC be the perpendicular drawn from O to AB.

We know, that the perpendicular to a chord, from the centre of a circle, bisects the chord.

Hence, radius of the circle is 5 cm.

Solution 3

Let AB be the chord and O be the centre of the circle.

Let OC be the perpendicular drawn from O to AB.

We know, that the perpendicular to a chord, from the centre of a circle, bisects the chord.

AC = CB

Solution 4

Let AB be the chord of length 24 cm and O be the centre of the circle.

Let OC be the perpendicular drawn from O to AB.

We know, that the perpendicular to a chord, from the centre of a circle, bisects the chord.

AC = CB = 12 cm

Solution 5

For the inner circle, BC is a chord and .

We know that the perpendicular to a chord, from the centre of a circle, bisects the chord.

BP = PC

For the outer circle, AD is the chord and.

We know that the perpendicular to a chord, from the centre of a circle, bisects the chord.

AP = PD

By Pythagoras Theorem,

OA2 = OP2 + AP2

=> AP2 = (34)2 – (16)2 = 900

=> AP = 30 cm

AB = AP – BP = 30 – 12 = 18 cm

Solution 6

Let O be the centre of the circle and AB and CD be the two parallel chords of length 30 cm and 16 cm respectively.

Drop OE and OF perpendicular on AB and CD from the centre O.

Solution 7

Since the distance between the chords is greater than the radius of the circle (15 cm), so the chords will be on the opposite sides of the centre.

Let O be the centre of the circle and AB and CD be the two parallel chords such that AB = 24 cm.

Let length of CD be 2x cm.

Drop OE and OF perpendicular on AB and CD from the centre O.

Solution 8

Solution 9

Let the radius of the circle be r cm.

Solution 10

Circle Exercise Ex. 17(B)

Solution 1

Solution 2

Solution 3

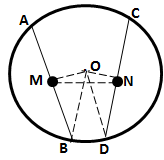
Solution 4

Drop OM and O’N perpendicular on AB and OM’ and O’N’ perpendicular on CD.

Solution 5

Drop OM and ON perpendicular on AB and CD.

Join OP, OB and OD.

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Circle Exercise Ex. 17(C)

Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

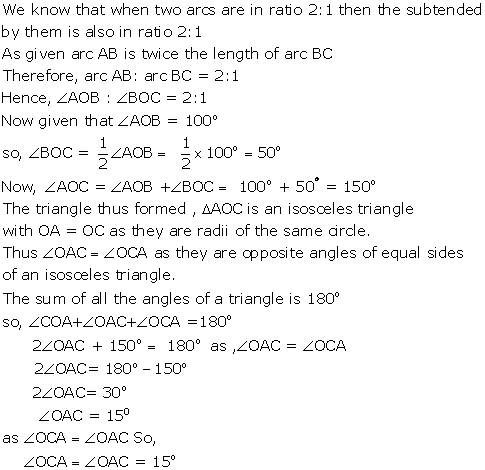
Circle Exercise Ex. 17(D)

Solution 1

Solution 2

Solution 3

So, the circle can have 0, 1 or 2 points in common.

The maximum number of common points is 2.

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10